What’s the difference between arithmetic and geometric returns?
Arithmetic returns are straightforward to calculate.
Add up the returns for each period and divide by the number of periods.
They are commonly used for simple return calculations.
In case 1 and case 2, we can see the arithmetic mean under constant 10% returns and 25% over the last 2 years, both result in arithmetic mean of 10%.


But, we discover that in case 2, the exit value is not equal to the exit value in case 1. Even though, the arithmetic means are the same.
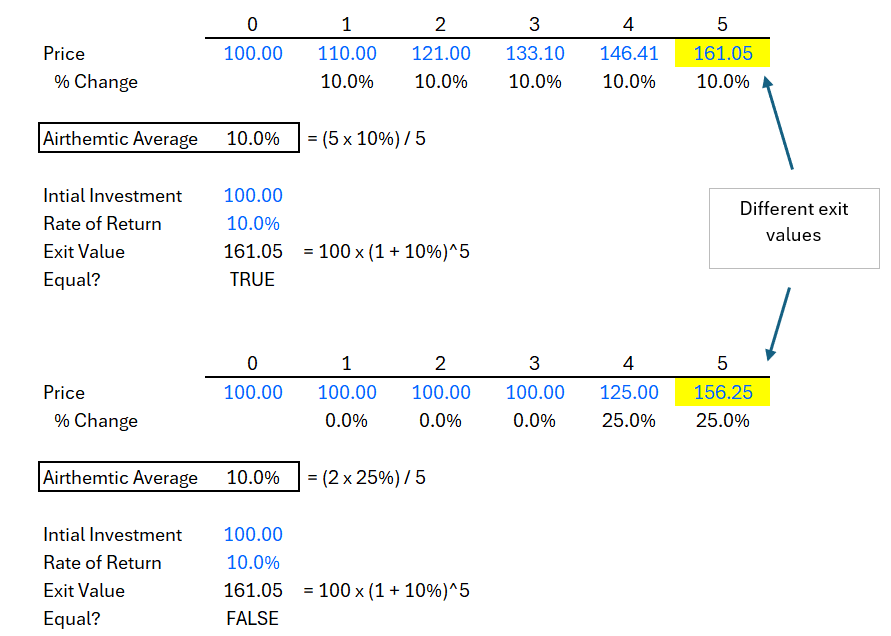
This is because compounding kicks in earlier in case 1. So returns compound on returns. Whereas in case 2, returns only kick in during the last 2 years, so there is much less time to compound.
Geometric returns consider the compounding effect of returns over time.
They provide a more accurate measure of investment growth.
In order to reach the equilibrium point, we can simply set the exit value equal in both case 1 and case 2, $161, and then back into the required return in the last 2 years.
This tells us that over the last 2 years, the investment must produce returns of 26.9%.

This is more than what is suggested by the simple average of 25%.
Why? Because returns earned later do not benefit as much from compounding.
Compounding requires time.
Internal Rate of Return (IRR) is a financial metric that uses geometric returns to evaluate the profitability of an investment or project.
Therefore, when returns are not constant, a simple average will not result in the same percentage as IRR.
When returns are received later, the IRR will fall short of the simple average.